SIGMOD 2022 ISUM
Published:
ISUM: Efficiently Compressing Large and Complex Workloads for Scalable Index Tuning. SIGMOD. 2022.
名称：ISUM: Efficiently Compressing Large and Complex Workloads for Scalable Index Tuning 概括：ISUM 针对的是工作负载压缩，定制于索引推荐场景。这篇工作的主要贡献点在于：区别对待工作负载里的每个查询，充分考虑查询与查询之间的依赖关系，从而按照权重加和的方式得到更有效的特征值。
问题形式化
工作负载：$W=\left{q_{1}, q_{2}, \ldots, q_{n}\right}$ 工作负载的代价：$C(W)=\sum_{i=1}^{n} C\left(q_{i}\right)$ 推荐出的索引集合（专业术语叫配置）：$I(W, A, m)=\left{i_{1}, i_{2}, \ldots, i_{m}\right}$，其中 $A$ 是 Index Advisor 这篇文章关注的重点就是，在$W$中挑选一个子集，也能让 $C(W)$最小化，即工作负载压缩。
本文的核心思想出现了！ 那就是 $W_k$，是从 $W$ 中选$k$个 query，且附上 weight，即$k$个 query-weight pair，后面会解释具体计算方法。并且他还有一招，就是估计代价的时候，用一个更高效的估计方法，这也会在后面说。
引申出一堆为了他的设计而作的指标/定义，如下：
Improvement：$\Delta=C(W)-C_{I\left(W_{k}, A, m\right)}(W)$，之后的定义里会忽略 A 和 m，这个 m 可以注意一下，也就是说索引的数量应该是超参。
对于$W$，和他们的 $C\left(q_{i}\right)$，我们要得到一个$k$，也就是拿到$k$个 query 和他们的“权重”（我觉得没必要在这个时候反复强调还有他们的权重，就直接说拿到$k$个代表性的 query 就行了）
这个$k$也不是空穴来风，他的目标是 $W_{k}=\underset{S_{k} \subset W}{\operatorname{argmax}} \Delta$
其实在这里强调提升值也没有什么意义，本质上就是 $W_{k}=\underset{S_{k} \subset W}{\operatorname{argmin}} C_{I\left(W_{k}\right)}(W)$
至此，问题形式化结束，问题应该描述的相当清楚。但是作者还是留了个很大的疑问：
他反复强调了两遍，他们这个工作在估计 **$C_{I\left(W_{k}\right)}(W)$时不需要调用优化器，这个怎么做？** 他们还强调了压缩时间不能过长，就是得到 **$k$ 个 query 的时间，值得关注。**
ISUM 的核心思路
如何挑一些索引来代表整个工作负载？
ISUM 选择一个查询，若他满足：
- 实用值（Utility）高，具体怎么算后文详细叙述；
- 当我们根据这个查询调优时，推荐的索引，能给其他查询带来增益。（Influence）
之前也说了，调用优化器估计代价是很昂贵的操作，ISUM 使用查询的 Cost 和诸如选择性之类的统计信息来估计在添加索引时降低查询开销的可能性【？？？不太懂，这个在传统数据库里不应该也是要估计的吗？】 “Specifically, a query with higher cost and more selective filters has higher potential for reduction in its cost “这是原文的话，这不是废话吗？ 要带着上述的问题去看看 Utility 的计算。
为了度量 Influence，ISUM 拿 query 的一些特征去表征这个 query，并且用【表大小，列所在的顺序位置、统计信息里的选择度】之类给这些特征赋权重。然后用 weighted Jaccard 去度量 query 之间相似度。两个 query 相似就代表了，对于其中一个 query 推荐了 A 索引，A索引也会增益另一个 query，这就是所谓的 Influence。
上述 Utility 和 Influence 计算的思想大致讲了，（虽然 Utility 就是废话），最后呢他会将 Utility 和 Influence 加一起定义为 benifit，我们挑高 benifit 的 query。
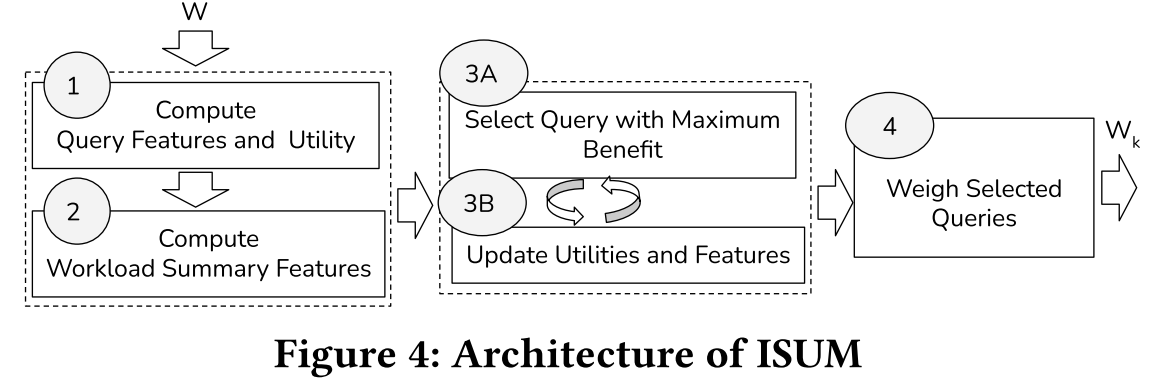
但是 两两之间做相似度这种做法不可取（all-pairs），作者提出一种 workload level 的表征技术，拿到 summary feature，达到线性时间的压缩【只吹牛，在这个地方又留坑了，据说在 Section 8 会讲】。总而言之，在这么模糊的描述中，图 4 给出了总体计算步骤，我感觉是讲的非常不清楚？
我们姑且推断一下，我们通过一个黑盒子，就是 summary feature 技术拿到了整个工作负载的信息，然后再更新 summary feature 里 query 的 benifit，最后拿到了 k 个 query。
填坑1：怎么解决代价估计昂贵的问题
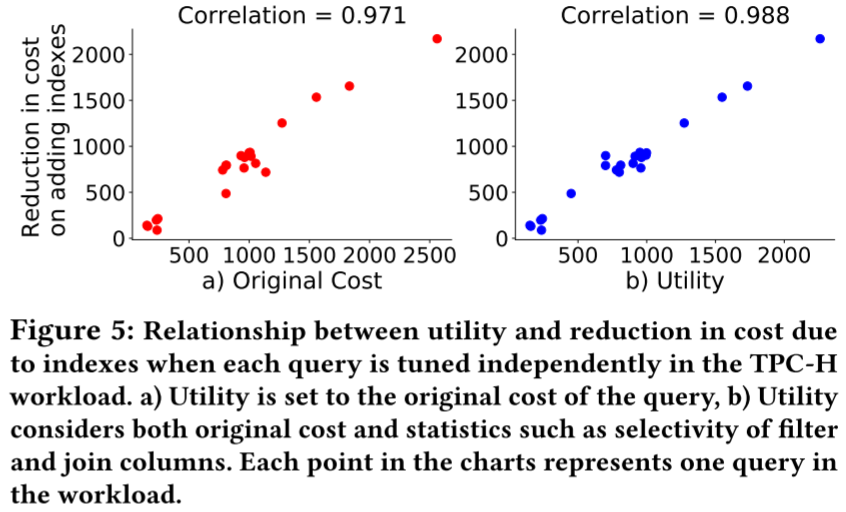
这张图表达了考虑了 selectivity 之后更好【可是很多相关工作都会考虑选择度，他的做法又有什么不同呢？我感觉这篇工作主要的贡献点就是有理有据，提出什么想法，怎么建模，都把他们实证考察了一番】。代价降低的潜力一般都是取决于 filter、join、order-by、group-by 算子，也包含 filter 和 join 的选择度。举例来说，如果这些算子的选择度是很高或很低的，那么代价降低的可能会很大，这是因为索引可以加速我们这种算子的性能。
Utility 的计算
初始代价：$C(q_i)$ 降低代价（估计出来）：$\triangle(q_i)$ 平均选择度 ：$Sel(q_i)$ 具体公式：$\triangle(q_i)=(1-Sel(q_i))\cdot C(q_i)$ 实用值计算公式：$U(q_i)=\frac{\triangle(q_i)}{\sum_{q_j\in W}\triangle(q_j) }$这时候我们假设，针对$q_i$的所有索引已经添加了 直观地说，如果查询具有更高的 U，则有助于整个工作负载的成本降低。
Influence 的计算
虽然相似性和提升性能之间存在一定的相关性，但具有最高相似性的查询并不一定会导致最大的改进
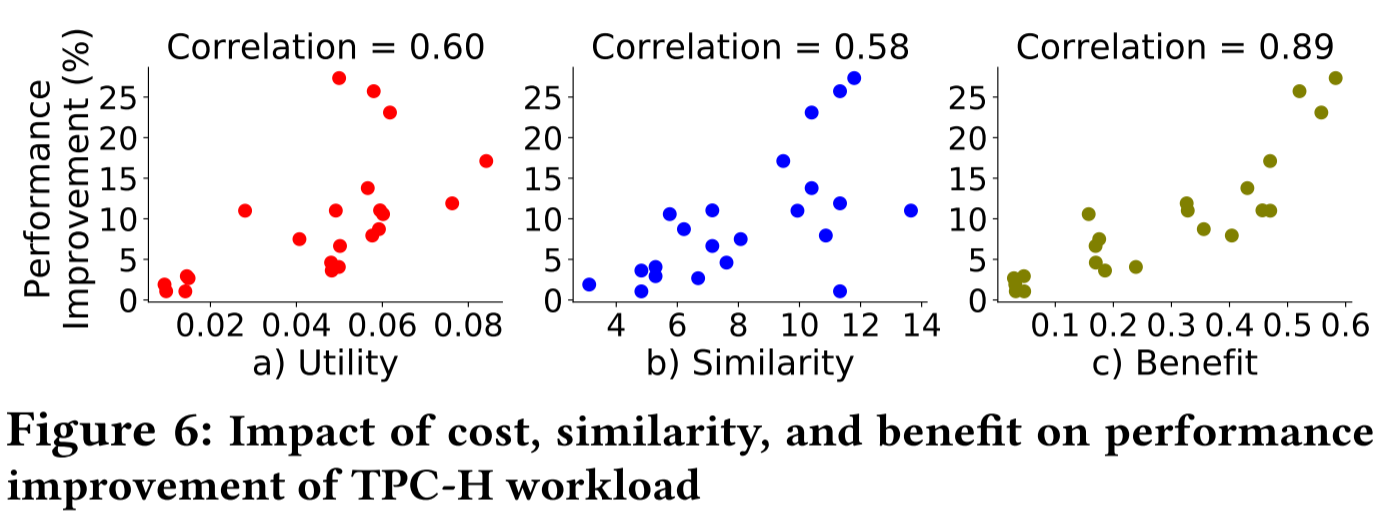
$F_{q_{i}}\left(q_{j}\right)=S\left(q_{i}, q_{j}\right) \times U\left(q_{j}\right), \forall q_{j} \notin W_{k}, q_{i} \in W_{k}$ 用相似度稀释一下 $q_j$ 的 U 值然后加进去，这个很好理解
$B\left(q_{i}\right)=U\left(q_{i}\right)+\sum_{q_{j} \in W-\left{q_{i}\right}} F_{q_{i}}\left(q_{j}\right)$ 结合之前说的 Utility，最后可以给单个 query 打分，即 Benefit
再结合图 6 的实验效果，就是用 Benefit 来衡量的话，相关性是更好的，本质上是考虑的信息更多，其他都是数学建模的事，但是这个建模相当简单，用相似度来作为权重做个累计权重和作为 Influence，然后 Influence + Utility = Benefit。
Similarity 的计算
上面也看到，Similarity 只是用来当做一个权重，但是度量方法是很多的。
Similarity using Candidate Indexes.: 大体思想是求两个索引推出的候选索引集的 Jaccard。但是还是需要一个 all-pair的思想。
Similarity using Indexable Columns： 类似，只是求的是可索引列集合的 Jaccard，但本人不太清楚这两个之间的量化区别，因为其实很多时候候选索引集和可索引列都是一样的。
怎么提取 indexable column
- filter
- join
- group-by
- order-by
Jaccard $S\left(q_{i}, q_{j}\right)=\frac{C_{q_{i}} \cap C_{q_{j}}}{C_{q_{i}} \cup C_{q_{j}}}$
然后作者又提出三种做法，比较了下
- Jaccard
- Weighted Jaccard (Rule-based)
- Weighted Jaccard (Stats-based)
当然选 d，这里可以当做黑盒子，太长的论述去描写几种很简单的相似性度量方法了。
终于到了 Benefit 的形式化
之前论述的角度都是非常独立的去考虑单个被选中的 query，但是压缩的工作负载一般不会是单元素集合，很可能是很多个，这就需要我们考虑 query 1 被选时的值，在 query_2 被选上时怎么更新的了。 $q_{j} \mid q_{i}$表示考虑了某个被选择来代表工作负载的查询 $q_i$的 influence 后更新的 $q_j$，假设有很多查询都被选了，我们需要去更新 $q_j$
更新 Utility $U\left(q_{j} \mid q_{i}\right)=U\left(q_{j}\right)-U\left(q_{j}\right) \times S\left(q_{i}, q_{j}\right)$
更新 feature $q_{j} \mid q_{i}=q_{i}-S\left(q_{i}, q_{j}\right)$
条件影响（Conditional Influence），更加形式化的概念 $F_{q \mid \pi(Q)}\left(q^{\prime} \mid \pi(Q)\right)=S\left(q\left|\pi(Q), q^{\prime}\right| \pi(Q)\right) \times U\left(q^{\prime} \mid \pi(Q)\right)$
追加：每个变量的计算 $F_{q \mid \pi(Q)}\left(q^{\prime}\right):=F_{q \mid \pi(Q)}\left(q^{\prime} \mid \pi(Q)\right),$ $S_{\pi(Q)}\left(q, q^{\prime}\right):=S\left(q\left|\pi(Q), q^{\prime}\right| \pi(Q)\right),$ $U_{\pi(Q)}\left(q^{\prime}\right):=U\left(q^{\prime} \mid \pi(Q)\right)$
综上，$F_{q \mid \pi(Q)}\left(q^{\prime}\right)=S_{\pi(Q)}\left(q, q^{\prime}\right) \times U_{\pi(Q)}\left(q^{\prime}\right)$
累计影响 $F_{\pi(Q)}\left(q^{\prime}\right)=\sum_{l=1}^{K} F_{q_{i_{l}} \mid q_{i_{1}}, \ldots, q_{i_{l-1}}}\left(q^{\prime}\right)$
回到最终目的，就是优化得到最大收益。 $W_{k}=\underset{S_{k} \subset W}{\operatorname{argmax}} B\left(S_{k}\right) .$
简化来说就是 $W_{k}=\underset{S_{k} \subset W}{\operatorname{argmax}}\left(\sum_{q_{l} \in W} F_{S_{k}}\left(q_{l}\right)\right) .$ 仍然是 NP-hard 问题，至此问题描述大致结束。
那么是如何降低的 Cost 估计的开销的呢？
回答这个问题就是，这个作者含蓄的表达了，这套建模就是反应了 cost reduction， 应该就不用去调用优化器了，但是代表性的 query 真的不用调用优化器去估算一下代价吗？保留这个疑问再往下看看。
压缩流程：一种 All-Pair 贪心的策略
- 开始是空集
- 纳入最大 conditional benefit 的 query
- All-pair 思想，同时考虑更新交互的 query
conditional benefit：$B_{\pi(Q)}(q)=U_{\pi(Q)}(q)+\sum_{q^{\prime} \in W-(Q \cup{q})} F_{q \mid \pi(Q)}\left(q^{\prime}\right)$ 直观地说，在每一个贪心步骤中，都会选择比工作负载中的其余查询具有最大条件益处的查询。选择查询后，我们更新未选择查询的查询特性和成本。
我感觉这个压缩流程比较基础，而且作者也会在下一章写如何对工作负载层面的 summary feature 做更新操作，这一章的内容就是在讲一个 baseline。
填坑 2：Workload Summary Features
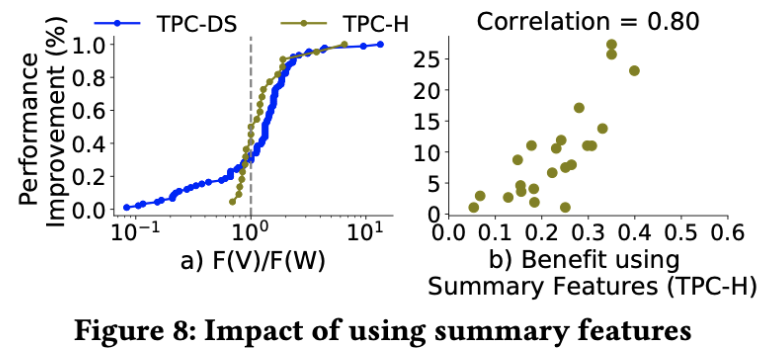一种简单的 summary 方法可以是对所有查询的查询特征做 sum 或 mean。但这种做法不好，因为他们把 query 们看成一样的，但事实上前面也说了，不同的 query 有不同的 U 值，所以要注意这个权重。
$F_{q_{s}}(W)=\sum_{q_{j} \in W-\left{q_{s}\right}} S\left(q_{s}, q_{j}\right) \times U\left(q_{j}\right)$ 代表了$q_s$在$W$中的 Influence。
$V_{i c}=q_{i c} \times U\left(q_{i}\right) .$ $q_i$中的$c$列的权重，$q_{ic}$代表 importance，也就是 c 列在 q_i 里的重要性，不知道怎么量化的。
$V_{c}=\sum_{q_{i} \in W} q_{i c} \times U\left(q_{i}\right)$ 这个其实就是最后得到的矩阵里面 c 列的值
$F_{q_{s}}(V)=S\left(q_{s}, V\right)$ 这个 V 本质就是 W 的特征了，所以我们后续都可以对这个 V 研究
对 W 做的操作改成对 V 的操作，使得原来的 all-pair 计算变得更加简单。 前面铺垫了特别多，就是可以用一句话说完：如果别人的工作是把工作负载直接特征化，就哪些列出现了多少次之类的；这个工作就是更精细的特征化，他考虑相似度和得分，最后得到一个 summary feature。
实验部分
实验把上述考虑的所有方法，就像叠积木一样，从最简单，到最精细，来对比。举个例子就是，考虑直接 sum 和考虑 Utility 的权重求和，这就是两个对比方法。 这样看来，这篇文章的工作写得好，但是有点过于啰嗦了，为什么不一上来就介绍一下别人是怎么拿到 summary feature，然后自己是改成考虑打分之后再 summary 呢？ 总结一下，别人的工作可能把 workload 里的每个 query 个体不去详细区分，不去判别重要性，他的工作就是很精细的给每个 query 个体打分，然后按照打分的权重和来作为某一列的值。举个例子就是，别人的工作 C 列出现 10次，就写 10，他可能是 1 * 1.9 + xxxxx + = xxx，这个过程是用 Utility 和 Similarity 来理论支撑的。